概要: 在50年代早期史威兹(Bryan Thwaites)担任中学教师时,他留给学生一项作业,要学生计算一组序列.其规则为:当某数为偶数时,则将该数除以2;若其为奇数,则先乘以3,然后加1.举个例子,如果给定的起始数字是7,则其后的推算如下:7奇数→7×3+1=2222偶数→22÷2=1111奇数→11×3+1=3434偶数→34÷2=17 17奇数→17×3+1=5252偶数→52÷2=2626偶数→26÷2=13 以此类推.很显然,如果遇到奇数,则下一个数会是一个较大的数,且为偶数,所以它在再下一个步骤中必定会被减半. 由当时学生们的探讨与史威兹本人的研究,他相信该序列终将出现1这个数字,然后又按照421421421 的顺序一直重复,所以可以将1视为该序列的终点.世界上有许多数学家试图
四年级奥数动手学数学:史威兹的推测,标签:四年级奥数题库,http://www.laixuea.com在50年代早期史威兹(Bryan Thwaites)担任中学教师时,他留给学生一项作业,要学生计算一组序列.其规则为:当某数为偶数时,则将该数除以2;若其为奇数,则先乘以3,然后加1.
举个例子,如果给定的起始数字是7,则其后的推算如下:
7奇数→7×3+1=22
22偶数→22÷2=11
11奇数→11×3+1=34
34偶数→34÷2=17
17奇数→17×3+1=52
52偶数→52÷2=26
26偶数→26÷2=13
以此类推.
很显然,如果遇到奇数,则下一个数会是一个较大的数,且为偶数,所以它在再下一个步骤中必定会被减半.
由当时学生们的探讨与史威兹本人的研究,他相信该序列终将出现1这个数字,然后又按照421421421 的顺序一直重复,所以可以将1视为该序列的终点.世界上有许多数学家试图证明这个猜想或是找出不同的终点,但截至目前尚无人成功.
现在请先将上面的序列继续完成,使该序列到达1为止,然后再自定一个不同的起始数字重复这个步骤.
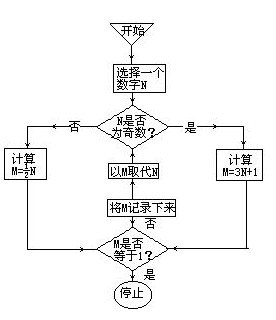
整个计算过程可以用流程图表示.
